The Sleeping Beauty Problem
Philosophy professors are failing a high school level word problem
The sleeping beauty problem could be a word problem for secondary school students. There are a few different statements of the problem, but this is the most common:
Sleeping Beauty volunteers to undergo the following experiment and is told all of the following details: On Sunday she will be put to sleep. Once or twice, during the experiment, Sleeping Beauty will be awakened, interviewed, and put back to sleep with an amnesia-inducing drug that makes her forget that awakening. A fair coin will be tossed to determine which experimental procedure to undertake:
If the coin comes up heads, Sleeping Beauty will be awakened and interviewed on Monday only.
If the coin comes up tails, she will be awakened and interviewed on Monday and Tuesday.
In either case, she will be awakened on Wednesday without interview and the experiment ends.
Any time Sleeping Beauty is awakened and interviewed she will not be able to tell which day it is or whether she has been awakened before. During the interview Sleeping Beauty is asked: "What is your credence now for the proposition that the coin landed heads?"
The special thing about this problem is that tenured academic professors can’t agree on what the answer should be. That may have to do, however, with those professors being philosophers and not statisticians.
The inventor of the problem, Adam Elga, as well as almost everyone who has subsequently published on it, are academic philosophers. Peter Winkler writes in his 2017 review on this:
Elga extracted the Sleeping Beauty problem (named by Robert Stalnaker) from Example 5 of Michele Piccione et al. [31], one of many papers in a volume of Games and Economic Behavior dedicated to a decision-theoretic problem known as “The Absent-Minded Driver.” Thus began a storm of arguments, papers, and blog comments, drawing in philosophers, mathematicians, and even physicists, then (seemingly) everyone.
Mathematicians and physicists don’t primarily study probability theory. In fact, undergraduate programs and even PhDs in those fields often completely avoid it. There is a group of tenured professors that do mainly study probability and its applications, however. These are the statisticians. But they seem to be absent from the discourse on this. Philosophers, of course, are the main participants here, and they study no mathematics whatsoever.
I am a self-taught amateur theoretical statistician, who is either currently reading at the PhD level or past it, depending on the area. In what follows, I’ll detail my ways of looking at the problem, and explain why they lead to the position known as double halferism. My approach also explains the source of the controversy, which is the definition of “credence” and how the meaning can vary from reader to reader (which I represent as thinking of different error functions).
My solution
To cut to the chase, it all depends on the definition of “credence.” Credence is closely related to risk functions. From Wikipedia::
Credence or degree of belief is a statistical term that expresses how much a person believes that a proposition is true.[1] As an example, a reasonable person will believe with close to 50% credence that a fair coin will land on heads the next time it is flipped (minus the probability that the coin lands on its edge). If the prize for correctly predicting the coin flip is $100, then a reasonable risk-neutral person will wager $49 on heads, but will not wager $51 on heads.
I propose that the idea of “the right credence” cannot be operationalised without an associated risk function (also called cost, loss, error, scoring etc) which is then optimized. If you do not have such a function, then “credence” is meaningless and there is no “right answer.” The optimal point of such a latent function is the source of any “right answer”.
From this you can immediately see why the two camps believe in 1/3 or 1/2 as the right answer. If the beauty is scored every time she guesses, the answer is 1/3. If the beauty is scored with respect to the most recent coinflip, the answer is 1/2. In other words, if you repeat the experiment 1000 times, and you flatten all the guesses, losing the information of which belonged to which experiment, then 1/3 is the optimal answer. If you retain the information of which guess is attached to which coinflip (when it is tails there will be 2 guesses for one coinflip), and you don’t double count the 2 guesses, then the right answer is 1/2.
import numpy as np
def get_heads_or_tails():
return 'H' if np.random.rand() < 0.5 else 'T'
def sleeper(p, guesses, flip_states):
flip = get_heads_or_tails()
flip_states.append(flip)
if flip == 'H':
guesses.append([p])
if flip == 'T':
guesses.append([p, p])
def avg(l):
return sum(l) / len(l) if l else 0
flip_map = {'H': 1, 'T': 0}
def score_within(guesses, flip_states):
flat_guesses = [avg(sublist) for sublist in guesses]
return avg([ (guess - flip_map[flip])**2 for guess,flip in zip(flat_guesses,flip_states)])
def score_overall(guesses, flip_states):
all_errors = []
for guess, flip in zip(guesses, flip_states):
error = [(sub_guess - flip_map[flip])**2 for sub_guess in guess]
all_errors.extend(error)
return avg(all_errors)
ps = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
within_scores = []
overall_scores = []
TIMES = 10000
for p in ps:
guesses = []
flip_states = []
for _ in range(TIMES):
sleeper(p, guesses, flip_states)
within_score = score_within(guesses, flip_states)
overall_score = score_overall(guesses, flip_states)
within_scores.append(within_score)
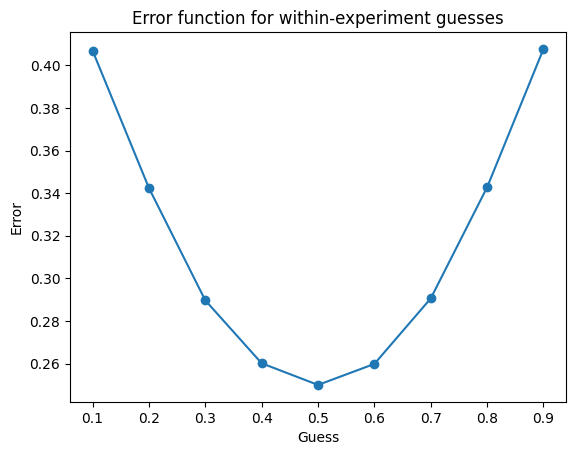
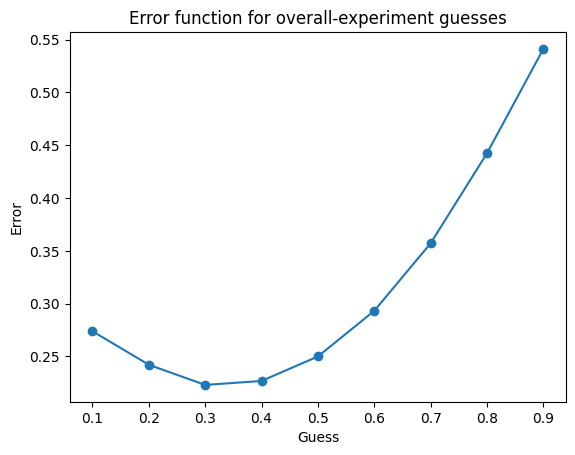
overall_scores.append(overall_score)Above is a simulation of the scenario. As you can see, we can judge the sleeper’s credence by two different functions. One averages her guess within one experiment into one guess (it could also truncate since she should always guess the same thing on every day, as she never knows the day or if she woke up before). This guess is then judged against the outcome of the single coinflip belonging to that experiment. This function (score_within) yields the optimal credence of 1/2.
The other function just takes all of the guesses and then scores them against the most recent coinflip. When the coin is tails, the experiment is essentially double weighted. Her guess is counted twice. Then getting the outcome wrong is twice as bad when the outcome was tails, you want to compensate by leaning towards tails. The scoring function is essentially weighted. It yields the 1/3 result.
You can see this using OLS as your optimizer as well.
SIZE = 500000 #large number gets rid of estimation noise, still runs <1sec
y = []
for i in range(SIZE):
flip = get_heads_or_tails()
if flip == 'H':
y.append(1)
else:
y.append(0)
y.append(0) # if this is commented out, it will give B = 0.5. If it is double counted, it gives B = 0.33
X = np.ones((len(y), 1))
b = np.linalg.inv(X.T @ X) @ X.T @ y
print(b)This takes a bit more theoretical statistics experience to understand than the earlier code, which is probably why philosophers haven’t thought of it, but if you regress a vector of 1s onto a vector of coin flips, you get a beta of 1/2. This means the optimal constant guess is 1/2. If you double count the tails, you get a beta of 1/3, meaning the optimal constant guess is 1/3 under double-counted tail flips. You can see this in the code with the second y.append(0) line. If it’s commented out, B=.5, if it stays in, B=.33.
This leads to an even simpler approach using maximum likelihood estimation. The beta here is the same as the MLE of the p parameter for coin flip column modeled as a Bernoulli random variable. This in turn is just the mean of the column. Quite simply, if you form the column by only writing down the result of each flip, the MLE is p=.5. If you double count tails, because she wakes up twice under tails and therefore “sees” tails twice, the MLE is p=.33. Which is more correct?
It’s clear to me that we’re asking sleeping beauty about the coin, and not punishing her for guessing wrong on each waking day. Thirders are wrongly using a weighted scoring function, double counting tails because she wakes twice under tails, while the natural scoring function yields the halfer position.
Bayes’ theorem
When the philosophers and non-statistician math people pull out the algebra on this topic, they usually stop at high school probability notation and the first theorem of probability that anybody learns, which is Bayes’ theorem. This yields a number of marginal, joint, and conditional probability values that are argued about in the literature. I’ll now show what my solution means in this language and why it makes sense.
Above is the classic Thirder argument. It correctly states that, 1/3 of the time the sleeper wakes up, it will be heads. Thus P(H) interpreted as the probability of the sleeper “observing” heads upon waking (this is a different problem than the one given) is 1/3. However, the sleeper double observes tails in this scenario. But this is a different problem than the one given; in reality the sleeper does not learn the day or the outcome and is judged with respect to the flip at the beginning of the week. Thus, the “flaw” is assuming P(H & M) and so on are greater than 0. In fact, by the problem set up, all of those joint probabilities are 0, since the sleeper never observes the day. The way the philosophers talk about the problem highlights the error. They talk as if the day is revealed, when in fact it is not.
Some halfers, including Lewis [25], dispute the claim that P(H |M) = 1/2—a hard position to maintain when you consider that the experimenters don’t need to flip the coin until Monday night. (How can SB’s credence in Heads be other than 1/2 if she knows the coin hasn’t been flipped yet?) Others (called “double-halfers”) concede that P(H |M) = 1/2, maintaining that SB’s credence in Heads doesn’t change when she hears it’s Monday. [she does not hear it’s Monday — she is not informed of the day, she is asked a credence and put back to sleep.]
Further symmetry arguments have been advanced. Modulo details, Dorr [10] and Arntzenius [2] suppose that regardless of the coin flip, SB will be awakened on both days, but in the event of Heads, SB will be told “Heads and Tuesday” 15 minutes after her Tuesday awakening. Then, for the first 15 minutes that SB is awake, “Heads and Monday,” “Heads and Tuesday,” “Tails and Monday,” and “Tails and Tuesday” are equiprobable by symmetry. After 15 minutes, when SB doesn’t get the “Heads and Tuesday” signal, she eliminates that option, and the other three possibilities must remain equiprobable.
P(U) is not the probability it is 0; from the Bayesian perspective, it’s the probability that the agent observes it is Tuesday. That is 0. The problem statement says “she will not be able to tell which day it is”. Even if it “is” Tuesday, she will never receive that signal. The philosophers have fallen for distractor information inside a high school word problem. This is negatively correlated with g, as it’s common on tests like the SAT.
Setting P(M) and P(U) to 0, the conditionals of them become undefined, like n/0. Their joint probabilities do not sum to 1 as the philiosopher says, so the last line does not follow.
What will happen is a single generic event W, which is waking. We want P(H|W), the probability of heads when she wakes up. We have P(H|W) = P(W|H)P(H)/P(W) by Bayes’ theorem. This simplifies to 1*1/2 / 1 which is 1/2, since by problem construction there will always be a generic waking with no memory of waking before experienced by the agent.
Penalized Sleeper
Let’s consider a modified problem where credence is operationalized in a way that makes the participant care about how right she is.
Sleeping beauty enters the experiment room. The researcher tells her, "we are going to flip this coin. If it's heads, we will wake you once. If it's tails, we wake you twice. The coin is fair. You will have no memory of being awoken no matter what. When you awake, you tell us your credence that the coin landed on heads".
With that sleeping beauty is prepared for her rest. "One last thing: you will be penalized in proportion to how wrong your credence is. Good luck!"
“Hold on, what does credence mean?” she asks.
The researcher responds, “we’re going to enter your soul into a multiverse where the experiment is repeated millions of times. If you guess 1/2, then half of the time your multiverse avatars will guess heads. If it’s 1/3, they will guess heads 1/3 of the time, and so on. They might get it wrong, but an avatar that was wrong in the opposite way cancels out the penalty. So if you guess heads and it was tails, as long as there is a corresponding tails guess for a heads, the guesses are swapped through the multiverse and no penalty accumulates. The number of multiverses is very large, and a small number of penalties is unnoticeable. But if your credence is off by even 1%, the penalties will accumulate and cross the noticeable threshold. You therefore should really want to get the answer right. Good luck!”
But the sleeper was very intelligent, so she asked one more question. “Is the penalty given right after the guess, or at the end of the experiment?”
If it’s given right after the guess, she guesses 1/3. If it’s given at the end, she guesses 1/2. This is because, suppose she wakes up on Monday and guesses incorrectly. If she guesses 1/2, somewhere out there another one of her guesses the opposite and the Monday penalty cancels out. But then one of those avatars wakes again and there is no cancellation penalty. Thus Tuesday penalties accumulate.
If the penalty is given at the end of the week, they all cancel under the 1/2 guess, since she is not double penalized for guessing the same wrong answer on both Monday and Tuesday.
If same-day (double) penalties are given, she must guess heads 1/3 of the time so that for every wrong heads guess, there is a corresponding wrong tails guess. Thus the penalties all cancel.
The problem statement is pretty clear; no penalty is mentioned but it is most natural to assume an intelligent beauty will have no variance in her guess. Her guess, even if stated twice, will be evaluated once against “the coin flip” at the end of the week. There is no double penalty. Thus the researcher would say “the penalty happens at the end of the week” and the rational sleeper will guess 1/2.