How genetically similar are siblings compared to their peers?

It depends on assortative mating

Last time, I showed that the variance among siblings is always half as much as their parent’s generation’s variance. And this doesn’t depend on assortative mating — it’s always true no matter how similar couples are.

However, a commenter pointed out that assortative mating will increase the variance of the kid’s generation. In math:

\(\mathbb{V}(Siblings) = \frac{1}{2}\mathbb{V}(Parents) \)

\(\mathbb{V}(Kids) \geq \mathbb{V}(Parents)\)

\(\implies \mathbb{V}(Siblings) \leq \frac{1}{2} \mathbb{V}(Kids)\)

It turned out on simulation that, in perfect assortative mating,

\(\mathbb{V}(Siblings) = \frac{1}{3}\mathbb{V}(Kids)\)

So at intermediate levels, the variance of siblings will be between 33% and 50% of the variance of their peers.

SIZE = 1000
ps = np.random.normal(.5,.15,SIZE)
ps[ps > 1] = .999
ps[ps < 0] = 0.01
fifties = [0.5 for i in range(SIZE)]

NUM_FAMS = 250
vars = []
parents = np.zeros((NUM_FAMS*2, SIZE))
all = np.zeros((NUM_FAMS*NUM_KIDS, SIZE))
for _ in range(NUM_FAMS):
    print(_/NUM_FAMS, end="\r")
    NUM_KIDS = 100
    m1 = np.random.binomial(1, ps)
    m2 = np.random.binomial(1, ps)
    f1 = np.random.binomial(1, ps)
    f2 = np.random.binomial(1, ps)
    parents[2*_] = m1 + m2
    parents[(2*_)+1] = m1 + m2
    kids = np.zeros((NUM_KIDS, SIZE))  # row: kid genome. col: genes
    for i in range(NUM_KIDS):
        samples = np.random.binomial(1, fifties)
        samples2 = np.random.binomial(1, fifties)
        kid1 = np.where(samples == 0, m1, m2)  # same as kid1 = np.array([m1[idx] for idx in range(SIZE) if (samples[idx] == 0) else (m2[idx]) ]) but written in C
        kid2 = np.where(samples2 == 0, m1, m2)  # make m1,m2 for perfect assortative mating, f1,f2 for random mating
        kids[i] = kid1 + kid2
    # Add all of the kids matrix to 'all'
    varst = np.var(kids, axis=0)
    vars.append( np.sum(varst))
    all[_*NUM_KIDS:(_+1)*NUM_KIDS] = kids  # Adding the kids to 'all'


# Compute the variance of the kids
kids_var = np.var(all, axis=0)
kids_var_sum = np.sum(kids_var)
vars.append(kids_var_sum)

# Convert vars to a numpy array
vars = np.array(vars)

# Compute the variance of the parents
parentvarl = np.var(parents, axis=0)
parentvar = np.sum(parentvarl)
sibvar = vars.mean()
print("Variance of kids:", kids_var_sum)
print("Variance of parents:", parentvar)
print('ratio', kids_var_sum/parentvar)
print(sibvar/kids_var_sum)
'''
OUTPUT:
Variance of kids: 682.1616028943927
Variance of parents: 455.08419200000003
ratio 1.498978902994707
0.3321545100723841
'''

Why does this happen? Each allele is the sum of the binary values at two loci:

\(A_i = L_{i,1} + L_{i,2}\)

and each gene score is the sum of all the allele values. So:

\(\mathbb{V}(Kids) = \frac{3}{2}\mathbb{V}(Parents) \implies \sum_i \mathbb{V}(A_i)_{Kids} = \frac{3}{2} \sum_i \mathbb{V}(A_i)_{Parents}\)

\(\mathbb{V}(A_i)_{Kids} = \frac{3}{2} \mathbb{V}(A_i)_{Parents} \implies \mathbb{V}(L_{i,1}) + \mathbb{V}(L_{i,2}) + 2Cov(L_{i,1}, L_{i,2}) = \frac{3}{2}( \mathbb{V}(L_{i,1}) + \mathbb{V}(L_{i,2}) )\)

This is because the covariance term is 0 in the parental generation, as the parents were assumed to be in Hardy-Weinberg equilibrium. We simplify to:

\(Cov(L_{i,1}, L_{i,2})_{kids} = \frac{1}{4}( \mathbb{V}(L_{i,1}) + \mathbb{V}(L_{i,2}) ) = \frac{1}{4} (pq + pq) = \frac{1}{2}pq\)

Under perfect assortative mating, this equation is true.

\(Cov(L_{i,1}, L_{i,2}) = \mathbb{E}[L_{i,1}L_{i,2}] - \mathbb{E}[L_{i,1}]\mathbb{E}[L_{i,2}] = \mathbb{P}(11) - p^2 \)

It turns out that

\( \mathbb{P}(11) = p^2 + \frac{1}{2}pq \)

So both sides of the equation are the same.

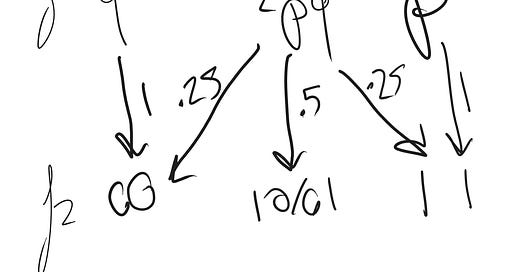
Why the last equation? Under perfect assortative mating, each homozygote always produces a batch of all homozygotes. But heterozygotes produce half heterozygotes and one quarter homozygotes of each type.

So the probability of being a heterozygote halves and

\(\mathbb{P}(11) = p^2 + \frac{1}{4}2pq\)

Under perfect assortment, the increment in terms of the original variance should halve each turn, approaching twice the original variance as the number of generations goes to infinity.

If you liked this, please subscribe. I may follow up with a post about the increase of variance at different mate correlations (that are more realistic than 1) as well as the relation of sibling to parent variance if parents are not at Hardy-Weinberg equilibrium.