The Mean IQ of SMPY Participants is Only 132

I've released a library for estimating latent traits like g from test scores and reliabilities. I apply this to the SMPY.

I released a Python package called bayesian_g_estimator. It features three functions: bayesian_g_estimator, ols_g_estimator, and brute_force_g_estimator. It can be installed using pip install bayesian_g_estimator. See the GitHub and the PyPI pages.

It works like this: you install the package with pip, import one of the functions, and pass in a list of (z_score, reliability) tuples for a person. It gives you the mean and standard deviation of the posterior distribution for their latent trait. See the PsyArxiv paper for more details.

In this article I’ll give a tutorial for use.

1. Install Python.

2. Run pip install bayesian_g_estimator

3. Import the function you want to use

   

4. Call the function. Scores should be a list of (z_score, reliability) tuples.

   

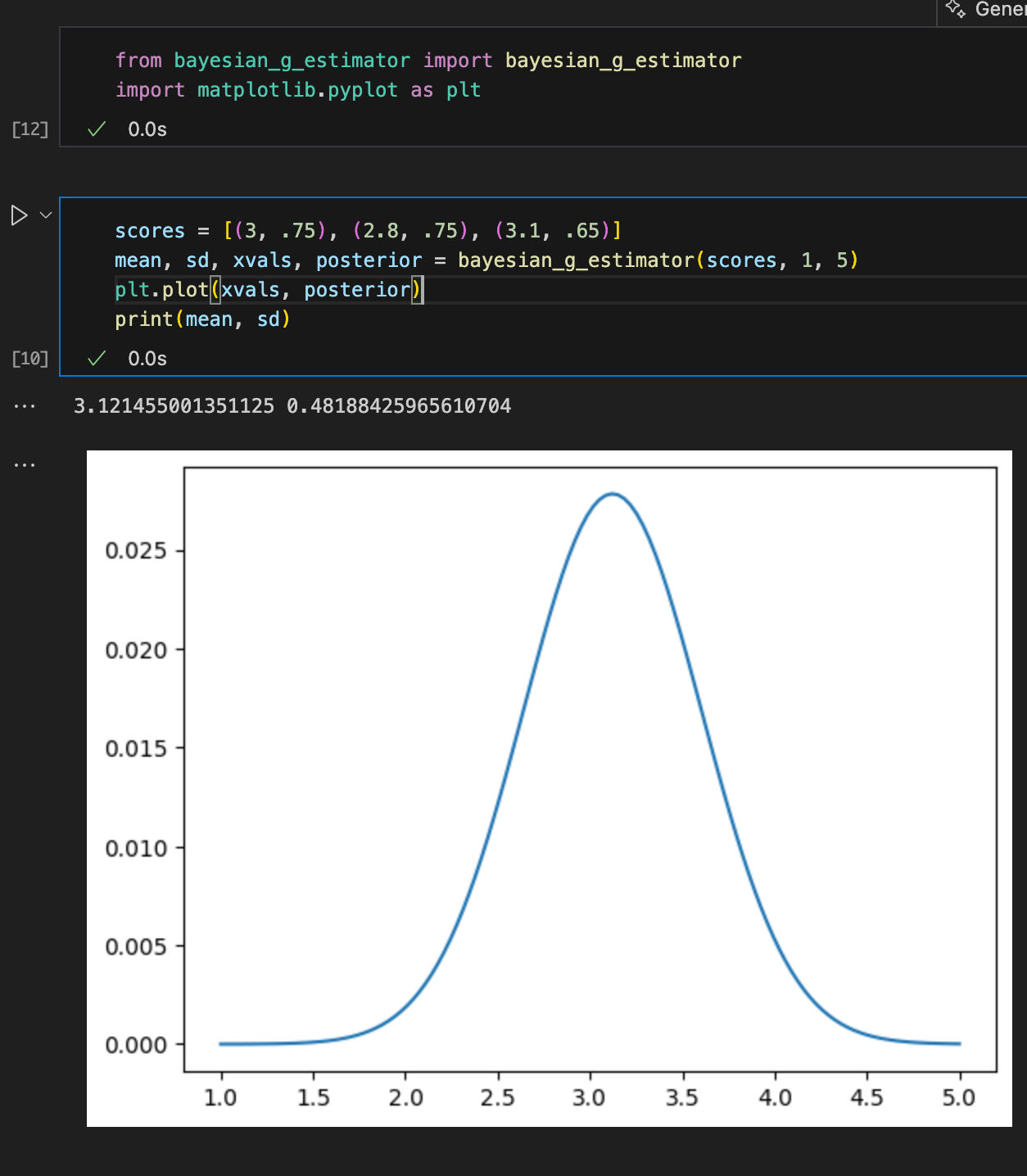
5. Graph results

   

   This distribution is the distribution of true scores given a huge set of people with those observed scores (3, 2.8, 3.1) on tests with those reliabilities (.75, .75, .65).

The Hard SMPY: 155 IQ?

There’s a study called the SMPY that claims to find 155 IQ people.

As you can see, the 1980 to 1983 cohort are supposedly the top 1 in 10,000, which corresponds to about 155 IQ.

However, a verbal SAT of 630 from 1983 is only 2.17 SD, or 132 IQ. The catch is that being 12 supposedly drops 10 to 15 points off your IQ.

Source

Supposing being 12 means your IQ is 12 points lower than your adult IQ, we add 12/15 = .8 to 2.17 to get 2.97 or 145 IQ. So they are 10 points high when they claim the sample minimum is 155. The hard SMPY should have a sample mean of at most 145.

But this doesn’t account for several factors: developmental variance, test reliability, and ability tilts. We can use our package to account for the first two, and we'll account for the last using custom code.

From Arthur Jensen, we get a correlation of .74 between IQ at 12 and 17 on the same test. This will incorporate test reliability as well as developmental variance. Being very charitable and saying the SAT has a reliability as high as the Stanford-Binet (~.89), we can just use .74 as the reliability of the SAT given at 12.

Why is the reliability lower at 12? The main reason is that the timing of puberty has a standard deviation of about 1 year. Taking this as a proxy for general developmental processes, we see that the median 12 year old is “theoretically 12”, but 2% are “theoretically 14” and another 2% are “theoretically 10”. Higher IQ scorers at 12 will tend to be on the better developed side. As adults, this variance is gone, so that advantageous component is too. Recall that we assumed the SMPY sample were all average developed 12 year old — this is not going to be the case, so using an empirically estimated test reliability for 12 year olds helps us find the midpoint between assuming they are average and assuming they are all “theoretically 14”.

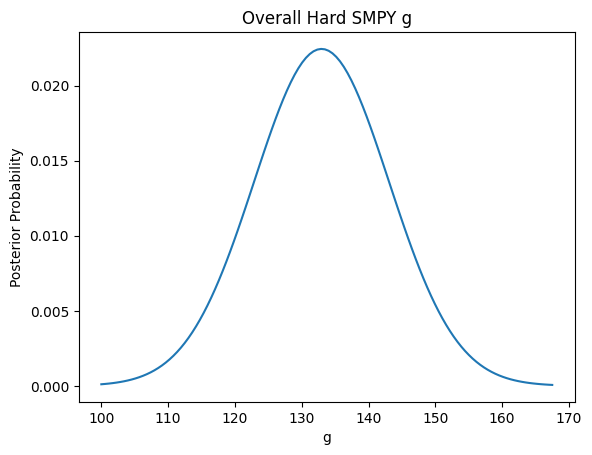
Throwing it all into the model, we get this as the true distribution of hard SMPY intelligences. The average is only 132, and many participants are sub 120 IQ!

If you think this is wrong, it’s 1) deduced from mathematical statistics, 2) validated against OLS and brute force methods.

The brute force method literally simulates a bunch of scorers with latent gs and find all the ones who get in the desired score range, then gives their mean g and the standard deviation of their g. It takes much more time to run than the other two methods, but it returns the same results.

The Jewish Subset

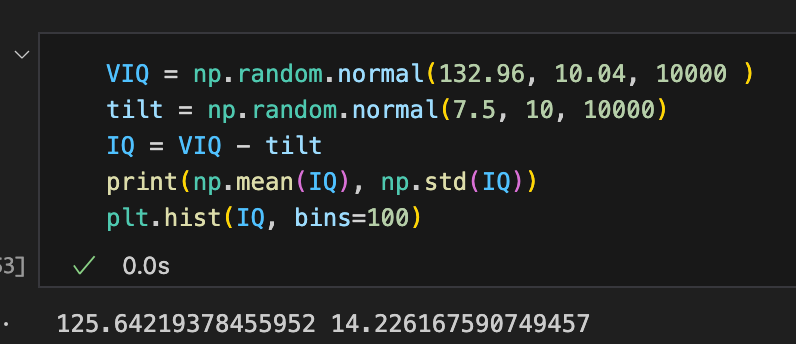
There were a lot of Jewish kids in the SMPY. Their IQ will not follow the same distribution as the gentile IQ: it will be much lower because of the pronounced verbal tilt of Jews. Two sources give a verbal IQ of Jews that is about 7.5 points higher than their overall mean intelligence.

On first pass we could say for the Jewish subset in the SMPY, the mean IQ should be 125. But the variance should increase, since some have higher verbal tilts than others.

From this paper we get a verbal tilt SD of about 10. Simulating, we get:

Most Jewish SMPY kids who were in the hard cohort have general intelligences in the 120s, or are more or less only the top 1 in 20.

This is probably why most of the Jewish SMPY kids in the online blogosphere write profusely, but with an underlying sophistication in reasoning, shape rotating, and quantitative ability of ~125, by my intuitive estimation.

This result also explains why midwestern kids were underrepresented in the SMPY. It wasn’t the special — it was mostly a development program for well connected coastal elites, not a scientific study. The principle researchers even interfered in the outcome of the study by writing letters of recommendation for the SMPY participants, helping them do better in life (the desired result was to clam that they were super-intelligent, and therefore do better in life than typical 125 IQ people).